PageRankのべき乗法、マルコフ連鎖の凝集
(「Google PageRankの数理」から)
2006年度の専攻科ゼミで参考にしたレビュー[1]の著者らによるより詳細な解説が、昨年(日本語版が)出版された[2]である。
「漸近的な収束の速さ(asymptonic rate of convergence)」:
-
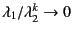 の速さ
の速さ
- Gが原始であるから
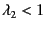
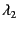 はスペクトラム(スペクトル半径?)が
はスペクトラム(スペクトル半径?)が
および
であるとき、
.
ただしSは確率的になるよう規格化した隣接行列。
.
- ウェブのリンク構造は可約であることが多いから最悪
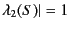 があり得て、
があり得て、
- つまり
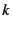 回の繰り返しに対して
回の繰り返しに対して
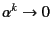 の速さで収束
の速さで収束
- 言い換えると、精度(スコアの桁数)を
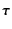 桁として、
桁として、
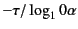 回
回
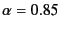 として2〜3桁なら50回
として2〜3桁なら50回
疎であるので…
リンク変更時の再計算の計算量削減のため。
- 確率分布をつかう?
- G(固有ベクトル
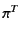 )より小さい、確率分布C(固有ベクトル
)より小さい、確率分布C(固有ベクトル )を用いる
)を用いる
- 歴史的には「ほとんど分離された連鎖の定常分布」を評価するのに使われてきた
- 状態空間Sを、
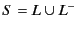 に分け(Lはリンクが更新された可能性が高いノード)
に分け(Lはリンクが更新された可能性が高いノード)
- (めんどくさいのでp.135参照)
- Sを打ち切り連鎖k個に分割
- Gを、「凝集された推移行列」or「結合行列」
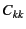 に縮約
に縮約
- 各々独立して解けて、「打ち切り分布」
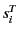 は
は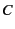
- (pp.137-138定理10.4.1)
本来は分割統治のためのものである。
が、以下などは、リンク構造に関係すると考えられ、クラスタリングのためにに使えないか。
指標: 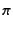 と
と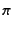 、
、 と
と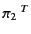 がどの程度近似できているか。
がどの程度近似できているか。
- 1
- Amy N.Langville, Carl D.Meyer ``A Survey of Eigenvector Methods for Information Retrieval'', SIAM Review Vol.47 No.1, pp.135-161 (2005).
- 2
- Amy N.Langville, Carl D.Meyer, 岩野 和生 (翻訳), 黒川 利明 (翻訳), 黒川 洋 (翻訳)『Google PageRankの数理―—最強検索エンジンのランキング手法を求めて』共立出版 (2009/10/10).
PageRankのべき乗法、マルコフ連鎖の凝集
(「Google PageRankの数理」から)
この文書はLaTeX2HTML 翻訳プログラム Version 2008 (1.71)
Copyright © 1993, 1994, 1995, 1996,
Nikos Drakos,
Computer Based Learning Unit, University of Leeds,
Copyright © 1997, 1998, 1999,
Ross Moore,
Mathematics Department, Macquarie University, Sydney.
を日本語化したもの(
2008 (1.71) JA patch-2.1beta1.12 版)
Copyright © 1998, 1999,
Kenshi Muto,
Debian Project.
Copyright © 2001-2010,
Shige TAKENO,
Niigata Inst.Tech.
を用いて生成されました。
コマンド行は以下の通りでした。:
latex2html seminar-20100503html.tex -split 0 -html_version 4.0 math -antialias.
翻訳は munenori によって 2010-06-04 に実行されました。
munenori
2010-06-04